Andrej Bauer, Martin Hofmann and Aleksandr Karbyshev. On Monadic Parametricity of Second-Order Functionals. In Frank Pfenning, editor, FoSSaCS, volume 7794 of Lecture Notes in Computer Science, pages 225-240, March 2013. Springer.
How can one rigorously specify that a given ML functional 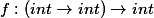 is pure, i.e.,
is pure, i.e., 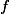 produces no computational effects except those produced by evaluation of its functional argument? In this paper, we introduce a semantic notion of monadic parametricity for second-order functionals which is a form of purity. We show that every monadically parametric
produces no computational effects except those produced by evaluation of its functional argument? In this paper, we introduce a semantic notion of monadic parametricity for second-order functionals which is a form of purity. We show that every monadically parametric 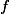 admits a question-answer strategy tree representation. We discuss possible applications of this notion, e.g., to the verification of generic fixpoint algorithms. The results are presented in two settings: a total set-theoretic setting and a partial domain-theoretic one. All proofs are formalized by means of the proof assistant Coq.
admits a question-answer strategy tree representation. We discuss possible applications of this notion, e.g., to the verification of generic fixpoint algorithms. The results are presented in two settings: a total set-theoretic setting and a partial domain-theoretic one. All proofs are formalized by means of the proof assistant Coq.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
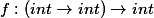 is pure, i.e.,
is pure, i.e., 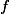 produces no computational effects except those produced by evaluation of its functional argument? In this paper, we introduce a semantic notion of monadic parametricity for second-order functionals which is a form of purity. We show that every monadically parametric
produces no computational effects except those produced by evaluation of its functional argument? In this paper, we introduce a semantic notion of monadic parametricity for second-order functionals which is a form of purity. We show that every monadically parametric 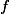 admits a question-answer strategy tree representation. We discuss possible applications of this notion, e.g., to the verification of generic fixpoint algorithms. The results are presented in two settings: a total set-theoretic setting and a partial domain-theoretic one. All proofs are formalized by means of the proof assistant Coq.
admits a question-answer strategy tree representation. We discuss possible applications of this notion, e.g., to the verification of generic fixpoint algorithms. The results are presented in two settings: a total set-theoretic setting and a partial domain-theoretic one. All proofs are formalized by means of the proof assistant Coq.