Javier Esparza, Thomas Gawlitza, Stefan Kiefer and Helmut Seidl. Approximative Methods for Monotone Systems of Min-Max-Polynomial Equations. In Luca Aceto, Ivan Damgård, Leslie Ann Goldberg, Magnús M. Halldórsson, Anna Ingólfsdóttir and Igor Walukiewicz, editors, Automata, Languages and Programming(1)Tack A: Algorithms, Automata, Complexity,and Games, volume 5125 of Lecture Notes in Computer Science, pages 698-710, Reykjavik, Iceland, July 2008. Springer.
A monotone system of min-max-polynomial equations (min-max-MSPE) over the variables 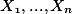 has for every
has for every 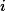 exactly one equation of the form
exactly one equation of the form 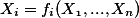 where each
where each 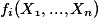 is an expression built up from polynomials with non-negative coefficients, minimum- and maximum-operators. The question of computing least solutions of min-max-MSPEs arises naturally in the analysis of recursive stochastic games [5,6,14]. Min-max-MSPEs generalize MSPEs for which convergence speed results of Newton’s method are established in [11,3]. We present the first methods for approximatively computing least solutions of min-max-MSPEs which converge at least linearly. Whereas the first one converges faster, a single step of the second method is cheaper. Furthermore, we compute ε-optimal positional strategies for the player who wants to maximize the outcome in a recursive stochastic game. This work was in part supported by the DFG project Algorithms for Software Model Checking.
is an expression built up from polynomials with non-negative coefficients, minimum- and maximum-operators. The question of computing least solutions of min-max-MSPEs arises naturally in the analysis of recursive stochastic games [5,6,14]. Min-max-MSPEs generalize MSPEs for which convergence speed results of Newton’s method are established in [11,3]. We present the first methods for approximatively computing least solutions of min-max-MSPEs which converge at least linearly. Whereas the first one converges faster, a single step of the second method is cheaper. Furthermore, we compute ε-optimal positional strategies for the player who wants to maximize the outcome in a recursive stochastic game. This work was in part supported by the DFG project Algorithms for Software Model Checking.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
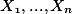 has for every
has for every 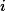 exactly one equation of the form
exactly one equation of the form 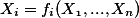 where each
where each 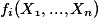 is an expression built up from polynomials with non-negative coefficients, minimum- and maximum-operators. The question of computing least solutions of min-max-MSPEs arises naturally in the analysis of recursive stochastic games [5,6,14]. Min-max-MSPEs generalize MSPEs for which convergence speed results of Newton’s method are established in [11,3]. We present the first methods for approximatively computing least solutions of min-max-MSPEs which converge at least linearly. Whereas the first one converges faster, a single step of the second method is cheaper. Furthermore, we compute ε-optimal positional strategies for the player who wants to maximize the outcome in a recursive stochastic game. This work was in part supported by the DFG project Algorithms for Software Model Checking.
is an expression built up from polynomials with non-negative coefficients, minimum- and maximum-operators. The question of computing least solutions of min-max-MSPEs arises naturally in the analysis of recursive stochastic games [5,6,14]. Min-max-MSPEs generalize MSPEs for which convergence speed results of Newton’s method are established in [11,3]. We present the first methods for approximatively computing least solutions of min-max-MSPEs which converge at least linearly. Whereas the first one converges faster, a single step of the second method is cheaper. Furthermore, we compute ε-optimal positional strategies for the player who wants to maximize the outcome in a recursive stochastic game. This work was in part supported by the DFG project Algorithms for Software Model Checking.