Thomas Gawlitza and Helmut Seidl. Games through Nested Fixpoints. In Ahmed Bouajjani and Oded Maler, editors, Computer Aided Verification, 21st International Conference, CAV 2009, Grenoble, France, June 26 - July 2, 2009. Proceedings, volume 5643 of Lecture Notes in Computer Science, pages 291-305, Grenoble, France, June 2009. Springer.

In this paper we consider two-player zero-sum payoff games on finite graphs, both in the deterministic as well as in the stochastic setting. In the deter- ministic setting, we consider total-payoff games which have been introduced as a refinement of mean-payoff games [18, 10]. In the stochastic setting, our class is a turn-based variant of liminf-payoff games [15, 16, 4]. In both settings, we pro- vide a non-trivial characterization of the values through nested fixpoint equations. The characterization of the values of liminf-payoff games moreover shows that solving liminf-payoff games is polynomial-time reducible to solving stochastic parity games. We construct practical algorithms for solving the occurring nested fixpoint equations based on strategy iteration. As a corollary we obtain that solv- ing deterministic total-payoff games and solving stochastic liminf-payoff games is in .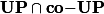

Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com