Andreas Goerdt and Helmut Seidl. Characterizing Complexity Classes by Higher Type Primitive Recursive Definitions, Part II. In Jürgen Dassow and Jozef Kelemen, editors, Aspects and Prospects of Theoretical Computer Scienc, volume 464 of Lecture Notes in Computer Science, pages 148-158, Smolenice, Czechoslovakia, November 1990. Springer.
Higher type primitive recursive definitions (also known as Gödel's system T) defining first-order functions (i.e. functions of type ind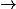 ...
...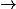 ind
ind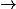 ind, ind for individuals, higher types occur in between) can be classified into an infinite syntactic hierarchy: A definition is in the n'th stage of this hierarchy, a so called rank-n-definition, iff n is an upper bound on the levels of the types occurring in it. We interpret these definitions over finite structures and show for
ind, ind for individuals, higher types occur in between) can be classified into an infinite syntactic hierarchy: A definition is in the n'th stage of this hierarchy, a so called rank-n-definition, iff n is an upper bound on the levels of the types occurring in it. We interpret these definitions over finite structures and show for 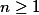 : Rank-(2n+2)-definitions characterize (in the sense of [Gu83], say) the complexity class DTIME
: Rank-(2n+2)-definitions characterize (in the sense of [Gu83], say) the complexity class DTIME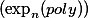 whereas rank-(2n+3)-definitions characterize DSPACE
whereas rank-(2n+3)-definitions characterize DSPACE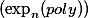 (here
(here 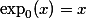 ,
, 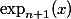
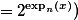 . This extends the results that rank-1-definitions characterize LOGSPACE [Gu83], rank-2-definitions characterize PTIME, rank-3-definitions characterize PSPACE, rank-4-definitions characterize EXPTIME [Go89a]
. This extends the results that rank-1-definitions characterize LOGSPACE [Gu83], rank-2-definitions characterize PTIME, rank-3-definitions characterize PSPACE, rank-4-definitions characterize EXPTIME [Go89a]
Reference: Bibtex The original publication is available at www.springerlink.com
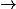 ...
...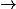 ind
ind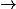 ind, ind for individuals, higher types occur in between) can be classified into an infinite syntactic hierarchy: A definition is in the n'th stage of this hierarchy, a so called rank-n-definition, iff n is an upper bound on the levels of the types occurring in it. We interpret these definitions over finite structures and show for
ind, ind for individuals, higher types occur in between) can be classified into an infinite syntactic hierarchy: A definition is in the n'th stage of this hierarchy, a so called rank-n-definition, iff n is an upper bound on the levels of the types occurring in it. We interpret these definitions over finite structures and show for 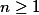 : Rank-(2n+2)-definitions characterize (in the sense of [Gu83], say) the complexity class DTIME
: Rank-(2n+2)-definitions characterize (in the sense of [Gu83], say) the complexity class DTIME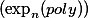 whereas rank-(2n+3)-definitions characterize DSPACE
whereas rank-(2n+3)-definitions characterize DSPACE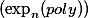 (here
(here 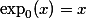 ,
, 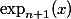
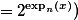 . This extends the results that rank-1-definitions characterize LOGSPACE [Gu83], rank-2-definitions characterize PTIME, rank-3-definitions characterize PSPACE, rank-4-definitions characterize EXPTIME [Go89a]
. This extends the results that rank-1-definitions characterize LOGSPACE [Gu83], rank-2-definitions characterize PTIME, rank-3-definitions characterize PSPACE, rank-4-definitions characterize EXPTIME [Go89a]