Markus Müller-Olm and Helmut Seidl. A Generic Framework for Interprocedural Analyses of Numerical Properties. In Franz Baader and Andrei Voronkov, editors, Logic for Programming, Artificial Intelligence, and Reasoning, volume 3452 of Lecture Notes in Computer Science, pages 432-432, Montevideo, Uruguay, March 2004. Springer.
Relations among program variables like 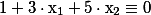 [224] have been called
[224] have been called 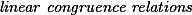 . Such a relation is valid at a program point iff it is satisfied by all reaching program states. Knowledge about non-trivial valid congruence relations is crucial for various aggressive program transformations. It can also form the backbone of a program correctness proof. In his seminal paper [1], Philippe Granger presents an intraprocedural analysis which is able to infer linear congruence relations between integer variables. For affine programs, i.e., programs where all assignments are affine expressions and branching is non-deterministic, Granger's analysis is
. Such a relation is valid at a program point iff it is satisfied by all reaching program states. Knowledge about non-trivial valid congruence relations is crucial for various aggressive program transformations. It can also form the backbone of a program correctness proof. In his seminal paper [1], Philippe Granger presents an intraprocedural analysis which is able to infer linear congruence relations between integer variables. For affine programs, i.e., programs where all assignments are affine expressions and branching is non-deterministic, Granger's analysis is 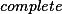 , i.e., infers
, i.e., infers 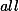 valid congruence relations between variables. No upper bound, though, has been proven for Granger's algorithm. Here, we present a variation of Granger's analysis which runs in polynomial time. Moreover, we provide an interprocedural extension of this algorithm. The polynomial algorithm as well as its interprocedural extension are obtained by means of multiple instances of a general framework for constructing interprocedural analyses of numerical properties. This framework can be used for different numerical domains such as fields or modular rings and thus also covers the interprocedural analyses of [2,3] where valid affine relations are inferred. We also indicate how the base technique can be extended to deal with equality guards in the interprocedural setting.
valid congruence relations between variables. No upper bound, though, has been proven for Granger's algorithm. Here, we present a variation of Granger's analysis which runs in polynomial time. Moreover, we provide an interprocedural extension of this algorithm. The polynomial algorithm as well as its interprocedural extension are obtained by means of multiple instances of a general framework for constructing interprocedural analyses of numerical properties. This framework can be used for different numerical domains such as fields or modular rings and thus also covers the interprocedural analyses of [2,3] where valid affine relations are inferred. We also indicate how the base technique can be extended to deal with equality guards in the interprocedural setting.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
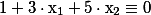 [224] have been called
[224] have been called 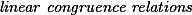 . Such a relation is valid at a program point iff it is satisfied by all reaching program states. Knowledge about non-trivial valid congruence relations is crucial for various aggressive program transformations. It can also form the backbone of a program correctness proof. In his seminal paper [1], Philippe Granger presents an intraprocedural analysis which is able to infer linear congruence relations between integer variables. For affine programs, i.e., programs where all assignments are affine expressions and branching is non-deterministic, Granger's analysis is
. Such a relation is valid at a program point iff it is satisfied by all reaching program states. Knowledge about non-trivial valid congruence relations is crucial for various aggressive program transformations. It can also form the backbone of a program correctness proof. In his seminal paper [1], Philippe Granger presents an intraprocedural analysis which is able to infer linear congruence relations between integer variables. For affine programs, i.e., programs where all assignments are affine expressions and branching is non-deterministic, Granger's analysis is 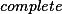 , i.e., infers
, i.e., infers 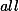 valid congruence relations between variables. No upper bound, though, has been proven for Granger's algorithm. Here, we present a variation of Granger's analysis which runs in polynomial time. Moreover, we provide an interprocedural extension of this algorithm. The polynomial algorithm as well as its interprocedural extension are obtained by means of multiple instances of a general framework for constructing interprocedural analyses of numerical properties. This framework can be used for different numerical domains such as fields or modular rings and thus also covers the interprocedural analyses of [2,3] where valid affine relations are inferred. We also indicate how the base technique can be extended to deal with equality guards in the interprocedural setting.
valid congruence relations between variables. No upper bound, though, has been proven for Granger's algorithm. Here, we present a variation of Granger's analysis which runs in polynomial time. Moreover, we provide an interprocedural extension of this algorithm. The polynomial algorithm as well as its interprocedural extension are obtained by means of multiple instances of a general framework for constructing interprocedural analyses of numerical properties. This framework can be used for different numerical domains such as fields or modular rings and thus also covers the interprocedural analyses of [2,3] where valid affine relations are inferred. We also indicate how the base technique can be extended to deal with equality guards in the interprocedural setting.