Markus Müller-Olm and Helmut Seidl. Analysis of Modular Arithmetic. In Shmuel Sagiv, editor, Programming Languages and Systems, volume 3444 of Lecture Notes in Computer Science, pages 46-60, Edinburgh, UK, April 2005. Springer.
We consider integer arithmetic modulo a power of 2 as provided by mainstream programming languages like Java or standard implementations of C. The difficulty here is that the ring 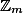 of integers modulo
of integers modulo 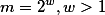 , has zero divisors and thus cannot be embedded into a field. Not withstanding that, we present intra- and inter-procedural algorithms for inferring for every program point u, affine relations between program variables valid at u. Our algorithms are not only sound but also
, has zero divisors and thus cannot be embedded into a field. Not withstanding that, we present intra- and inter-procedural algorithms for inferring for every program point u, affine relations between program variables valid at u. Our algorithms are not only sound but also 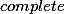 in that they detect
in that they detect 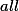 valid affine relations. Moreover, they run in time linear in the program size and polynomial in the number of program variables and can be implemented by using the same modular integer arithmetic as the target language to be analyzed.
valid affine relations. Moreover, they run in time linear in the program size and polynomial in the number of program variables and can be implemented by using the same modular integer arithmetic as the target language to be analyzed.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
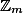 of integers modulo
of integers modulo 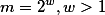 , has zero divisors and thus cannot be embedded into a field. Not withstanding that, we present intra- and inter-procedural algorithms for inferring for every program point u, affine relations between program variables valid at u. Our algorithms are not only sound but also
, has zero divisors and thus cannot be embedded into a field. Not withstanding that, we present intra- and inter-procedural algorithms for inferring for every program point u, affine relations between program variables valid at u. Our algorithms are not only sound but also 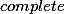 in that they detect
in that they detect 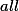 valid affine relations. Moreover, they run in time linear in the program size and polynomial in the number of program variables and can be implemented by using the same modular integer arithmetic as the target language to be analyzed.
valid affine relations. Moreover, they run in time linear in the program size and polynomial in the number of program variables and can be implemented by using the same modular integer arithmetic as the target language to be analyzed.