Markus Müller-Olm and Helmut Seidl. Analysis of modular arithmetic. ACM Trans. Program. Lang. Syst., 29(5), 2007.
We consider integer arithmetic modulo a power of 2 as provided by mainstream programming languages like Java or standard implementations of C. The difficulty here is that, for w > 1, the ring 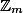 of integers modulo
of integers modulo 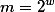 ,
,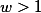 has zero divisors and thus cannot be embedded into a field. Not withstanding that, we present intra- and interprocedural algorithms for inferring for every program point
has zero divisors and thus cannot be embedded into a field. Not withstanding that, we present intra- and interprocedural algorithms for inferring for every program point 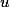 affine relations between program variables valid at
affine relations between program variables valid at 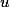 . If conditional branching is replaced with nondeterministic branching, our algorithms are not only sound but also complete in that they detect all valid affine relations in a natural class of programs. Moreover, they run in time linear in the program size and polynomial in the number of program variables and can be implemented by using the same modular integer arithmetic as the target language to be analyzed. We also indicate how our analysis can be extended to deal with equality guards, even in an interprocedural setting.
. If conditional branching is replaced with nondeterministic branching, our algorithms are not only sound but also complete in that they detect all valid affine relations in a natural class of programs. Moreover, they run in time linear in the program size and polynomial in the number of program variables and can be implemented by using the same modular integer arithmetic as the target language to be analyzed. We also indicate how our analysis can be extended to deal with equality guards, even in an interprocedural setting.
Download: PDF Reference: Bibtex
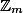 of integers modulo
of integers modulo 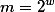 ,
,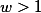 has zero divisors and thus cannot be embedded into a field. Not withstanding that, we present intra- and interprocedural algorithms for inferring for every program point
has zero divisors and thus cannot be embedded into a field. Not withstanding that, we present intra- and interprocedural algorithms for inferring for every program point 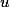 affine relations between program variables valid at
affine relations between program variables valid at 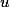 . If conditional branching is replaced with nondeterministic branching, our algorithms are not only sound but also complete in that they detect all valid affine relations in a natural class of programs. Moreover, they run in time linear in the program size and polynomial in the number of program variables and can be implemented by using the same modular integer arithmetic as the target language to be analyzed. We also indicate how our analysis can be extended to deal with equality guards, even in an interprocedural setting.
. If conditional branching is replaced with nondeterministic branching, our algorithms are not only sound but also complete in that they detect all valid affine relations in a natural class of programs. Moreover, they run in time linear in the program size and polynomial in the number of program variables and can be implemented by using the same modular integer arithmetic as the target language to be analyzed. We also indicate how our analysis can be extended to deal with equality guards, even in an interprocedural setting.