Flemming Nielson, Hanne Riis Nielson and Helmut Seidl. Normalizable Horn Clauses, Strongly Recognizable Relations, and Spi. In Manuel V. Hermenegildo and Germán Puebla, editors, Static Analysis, volume 2477 of Lecture Notes in Computer Science, pages 20-35, Madrid, Spain, September 2002. Springer.
We exhibit a rich class of Horn clauses, which we call 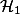 , whose least models, though possibly infinite, can be computed effectively. We show that the least model of an
, whose least models, though possibly infinite, can be computed effectively. We show that the least model of an 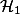 clause consists of so-called strongly recognizable relations and present an exponential normalization procedure to compute it. In order to obtain a practical tool for program analysis, we identify a restriction of
clause consists of so-called strongly recognizable relations and present an exponential normalization procedure to compute it. In order to obtain a practical tool for program analysis, we identify a restriction of 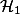 clauses, which we call
clauses, which we call 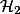 , where the least models can be computed in polynomial time. This fragment still allows to express, e.g., Cartesian product and transitive closure of relations. Inside
, where the least models can be computed in polynomial time. This fragment still allows to express, e.g., Cartesian product and transitive closure of relations. Inside 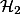 , we exhibit a fragment
, we exhibit a fragment 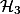 where normalization is even cubic. We demonstrate the usefulness of our approach by deriving a cubic control-flow analysis for the Spi calculus [1] as presented in [14].
where normalization is even cubic. We demonstrate the usefulness of our approach by deriving a cubic control-flow analysis for the Spi calculus [1] as presented in [14].
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
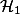 , whose least models, though possibly infinite, can be computed effectively. We show that the least model of an
, whose least models, though possibly infinite, can be computed effectively. We show that the least model of an 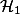 clause consists of so-called strongly recognizable relations and present an exponential normalization procedure to compute it. In order to obtain a practical tool for program analysis, we identify a restriction of
clause consists of so-called strongly recognizable relations and present an exponential normalization procedure to compute it. In order to obtain a practical tool for program analysis, we identify a restriction of 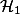 clauses, which we call
clauses, which we call 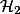 , where the least models can be computed in polynomial time. This fragment still allows to express, e.g., Cartesian product and transitive closure of relations. Inside
, where the least models can be computed in polynomial time. This fragment still allows to express, e.g., Cartesian product and transitive closure of relations. Inside 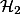 , we exhibit a fragment
, we exhibit a fragment 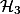 where normalization is even cubic. We demonstrate the usefulness of our approach by deriving a cubic control-flow analysis for the Spi calculus [1] as presented in [14].
where normalization is even cubic. We demonstrate the usefulness of our approach by deriving a cubic control-flow analysis for the Spi calculus [1] as presented in [14].