Oded Padon, Neil Immerman, Sharon Shoham, Aleksandr Karbyshev and Mooly Sagiv. Decidability of Inferring Inductive Invariants. Principles of Programming Languages, SIGPLAN, St. Petersburg, Florida, USA, January 2016. ACM.
Induction is a successful approach for verification of hardware and software systems. A common practice is to model a system using logical formulas, and then use a decision procedure to verify that some logical formula is an inductive safety invariant for the system. A key ingredient in this approach is coming up with the inductive invariant, which is known as invariant inference. This is a major difficulty, and it is often left for humans or addressed by sound but incomplete abstract interpretation. This paper is motivated by the problem of inductive invariants in shape analysis and in distributed protocols. This paper approaches the general problem of inferring first-order inductive invariants by restricting the language 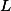 of candidate invariants. Notice that the problem of invariant inference in a restricted language
of candidate invariants. Notice that the problem of invariant inference in a restricted language 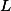 differs from the safety problem, since a system may be safe and still not have any inductive invariant in
differs from the safety problem, since a system may be safe and still not have any inductive invariant in 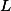 that proves safety. Clearly, if
that proves safety. Clearly, if 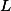 is finite (and if testing an inductive invariant is decidable), then inferring invariants in
is finite (and if testing an inductive invariant is decidable), then inferring invariants in 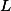 is decidable. This paper presents some interesting cases when inferring inductive invariants in
is decidable. This paper presents some interesting cases when inferring inductive invariants in 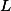 is decidable even when
is decidable even when 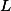 is an infinite language of universal formulas. Decidability is obtained by restricting
is an infinite language of universal formulas. Decidability is obtained by restricting 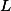 and defining a suitable well-quasi-order on the state space. We also present some undecidability results that show that our restrictions are necessary. We further present a framework for systematically constructing infinite languages while keeping the invariant inference problem decidable. We illustrate our approach by showing the decidability of inferring invariants for programs manipulating linked-lists, and for distributed protocols.
and defining a suitable well-quasi-order on the state space. We also present some undecidability results that show that our restrictions are necessary. We further present a framework for systematically constructing infinite languages while keeping the invariant inference problem decidable. We illustrate our approach by showing the decidability of inferring invariants for programs manipulating linked-lists, and for distributed protocols.
Download: PDF Reference: Bibtex
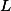 of candidate invariants. Notice that the problem of invariant inference in a restricted language
of candidate invariants. Notice that the problem of invariant inference in a restricted language 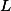 differs from the safety problem, since a system may be safe and still not have any inductive invariant in
differs from the safety problem, since a system may be safe and still not have any inductive invariant in 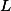 that proves safety. Clearly, if
that proves safety. Clearly, if 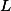 is finite (and if testing an inductive invariant is decidable), then inferring invariants in
is finite (and if testing an inductive invariant is decidable), then inferring invariants in 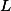 is decidable. This paper presents some interesting cases when inferring inductive invariants in
is decidable. This paper presents some interesting cases when inferring inductive invariants in 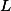 is decidable even when
is decidable even when 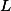 is an infinite language of universal formulas. Decidability is obtained by restricting
is an infinite language of universal formulas. Decidability is obtained by restricting 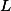 and defining a suitable well-quasi-order on the state space. We also present some undecidability results that show that our restrictions are necessary. We further present a framework for systematically constructing infinite languages while keeping the invariant inference problem decidable. We illustrate our approach by showing the decidability of inferring invariants for programs manipulating linked-lists, and for distributed protocols.
and defining a suitable well-quasi-order on the state space. We also present some undecidability results that show that our restrictions are necessary. We further present a framework for systematically constructing infinite languages while keeping the invariant inference problem decidable. We illustrate our approach by showing the decidability of inferring invariants for programs manipulating linked-lists, and for distributed protocols.