Helmut Seidl, Thomas Schwentick, Anca Muscholl and Peter Habermehl. Counting in Trees for Free. In Josep Díaz, Juhani Karhumäki, Arto Lepistö and Donald Sannella, editors, Automata, Languages and Programming, volume 3142 of Lecture Notes in Computer Science, pages 1136-1149, Turku, Finland, July 2004. Springer.
It is known that MSO logic for ordered unranked trees is undecidable if Presburger constraints are allowed at children of nodes. We show here that a decidable logic is obtained if we use a modal fixpoint logic instead. We present a characterization of this logic by means of 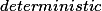 Presburger tree automata and show how it can be used to express numerical document queries. Surprisingly, the complexity of satisfiability for the extended logic is asymptotically the same as for the original fixpoint logic. The non-emptiness for Presburger tree automata (PTA) is pspace -complete, which is moderate given that it is already pspace-hard to test whether the complement of a regular expression is non-empty. We also identify a subclass of PTAs with a tractable non-emptiness problem. Further, to decide whether a tree
Presburger tree automata and show how it can be used to express numerical document queries. Surprisingly, the complexity of satisfiability for the extended logic is asymptotically the same as for the original fixpoint logic. The non-emptiness for Presburger tree automata (PTA) is pspace -complete, which is moderate given that it is already pspace-hard to test whether the complement of a regular expression is non-empty. We also identify a subclass of PTAs with a tractable non-emptiness problem. Further, to decide whether a tree 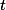 satisfies a formula
satisfies a formula 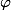 is polynomial in the size of
is polynomial in the size of 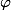 and linear in the size of
and linear in the size of 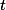 . A technical construction of independent interest is a
. A technical construction of independent interest is a 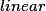 time construction of a Presburger formula for the Parikh image of a regular language.
time construction of a Presburger formula for the Parikh image of a regular language.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
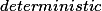 Presburger tree automata and show how it can be used to express numerical document queries. Surprisingly, the complexity of satisfiability for the extended logic is asymptotically the same as for the original fixpoint logic. The non-emptiness for Presburger tree automata (PTA) is pspace -complete, which is moderate given that it is already pspace-hard to test whether the complement of a regular expression is non-empty. We also identify a subclass of PTAs with a tractable non-emptiness problem. Further, to decide whether a tree
Presburger tree automata and show how it can be used to express numerical document queries. Surprisingly, the complexity of satisfiability for the extended logic is asymptotically the same as for the original fixpoint logic. The non-emptiness for Presburger tree automata (PTA) is pspace -complete, which is moderate given that it is already pspace-hard to test whether the complement of a regular expression is non-empty. We also identify a subclass of PTAs with a tractable non-emptiness problem. Further, to decide whether a tree 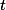 satisfies a formula
satisfies a formula 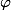 is polynomial in the size of
is polynomial in the size of 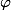 and linear in the size of
and linear in the size of 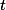 . A technical construction of independent interest is a
. A technical construction of independent interest is a 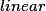 time construction of a Presburger formula for the Parikh image of a regular language.
time construction of a Presburger formula for the Parikh image of a regular language.