Helmut Seidl. Parameter Reduction of Higher Level Grammars. Theor. Comput. Sci., 55(1):47-85, 1987.
A higher level (OI-)grammar is called terminating, if for every accessible term 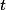 there is at least one terminal term which can be derived from
there is at least one terminal term which can be derived from 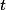 . A grammar is called parameter-reduced, if it is terminating and has no superfluous parameters. For every grammar
. A grammar is called parameter-reduced, if it is terminating and has no superfluous parameters. For every grammar 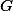 of level
of level 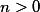 which generates at least one term we construct grammars
which generates at least one term we construct grammars 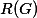 and
and 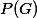 such that
such that 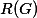 and
and 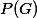 generate the same language as G but are terminating and paramter-reduced, respectively. We introduce a hierarchy of restrictions to the deletion capability of the grammars which allow a gradual decrease in the complexity of the algorithms from n-iterated exponential time to polynomial time.
generate the same language as G but are terminating and paramter-reduced, respectively. We introduce a hierarchy of restrictions to the deletion capability of the grammars which allow a gradual decrease in the complexity of the algorithms from n-iterated exponential time to polynomial time.
Download: PDF Reference: Bibtex
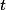 there is at least one terminal term which can be derived from
there is at least one terminal term which can be derived from 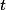 . A grammar is called parameter-reduced, if it is terminating and has no superfluous parameters. For every grammar
. A grammar is called parameter-reduced, if it is terminating and has no superfluous parameters. For every grammar 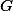 of level
of level 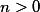 which generates at least one term we construct grammars
which generates at least one term we construct grammars 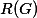 and
and 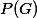 such that
such that 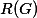 and
and 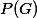 generate the same language as G but are terminating and paramter-reduced, respectively. We introduce a hierarchy of restrictions to the deletion capability of the grammars which allow a gradual decrease in the complexity of the algorithms from n-iterated exponential time to polynomial time.
generate the same language as G but are terminating and paramter-reduced, respectively. We introduce a hierarchy of restrictions to the deletion capability of the grammars which allow a gradual decrease in the complexity of the algorithms from n-iterated exponential time to polynomial time.