Helmut Seidl. On the Finite Degree of Ambiguity of Finite Tree Automata. In János Csirik, János Demetrovics and Ferenc Gécseg, editors, Fundamentals of Computation Theory, volume 380 of Lecture Notes in Computer Science, pages 395-404, Szeged, Hungary, August 1989. Springer.
The degree of ambiguity of a finite tree automaton 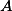 , da(
, da(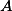 ), is the maximal number of different accepting computations of
), is the maximal number of different accepting computations of 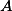 for any possible input tree. We show: it can be decided in polynomial time whether or not da(
for any possible input tree. We show: it can be decided in polynomial time whether or not da(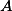 )
)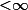 . We give two criteria characterizing an infinite degree of ambiguity and derive the following fundamental properties of an finite tree automaton
. We give two criteria characterizing an infinite degree of ambiguity and derive the following fundamental properties of an finite tree automaton 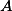 with
with 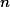 states and rank
states and rank 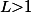 having a finite degree of ambiguity: for every input tree
having a finite degree of ambiguity: for every input tree 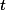 there is a input tree
there is a input tree 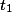 of depth less than
of depth less than 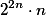 ! having the same number of accepting computations; the degree of ambiguity of
! having the same number of accepting computations; the degree of ambiguity of 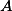 is bounded by
is bounded by 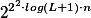 .
.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
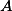 , da(
, da(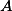 ), is the maximal number of different accepting computations of
), is the maximal number of different accepting computations of 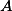 for any possible input tree. We show: it can be decided in polynomial time whether or not da(
for any possible input tree. We show: it can be decided in polynomial time whether or not da(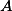 )
)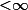 . We give two criteria characterizing an infinite degree of ambiguity and derive the following fundamental properties of an finite tree automaton
. We give two criteria characterizing an infinite degree of ambiguity and derive the following fundamental properties of an finite tree automaton 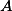 with
with 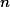 states and rank
states and rank 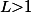 having a finite degree of ambiguity: for every input tree
having a finite degree of ambiguity: for every input tree 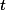 there is a input tree
there is a input tree 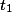 of depth less than
of depth less than 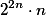 ! having the same number of accepting computations; the degree of ambiguity of
! having the same number of accepting computations; the degree of ambiguity of 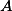 is bounded by
is bounded by 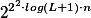 .
.