Helmut Seidl. Finite Tree Automata with Cost Functions. In Jean-Claude Raoult, editor, Trees in Algebra and Programming, volume 581 of Lecture Notes in Computer Science, pages 279-299, Rennes, France, February 1992. Springer.
Cost functions for tree automata are mappings from transitions to (tuples of) polynomials over some semiring. We consider four semirings, namely 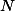 the semiring of nonnegative integers,
the semiring of nonnegative integers, 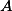 the ldquoarctical semiringrdquo,
the ldquoarctical semiringrdquo, 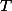 the tropical semiring and
the tropical semiring and 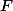 the semiring of finite subsets of nonnegative integers. We show: for semirings
the semiring of finite subsets of nonnegative integers. We show: for semirings 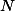 and
and 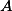 it is decidable in polynomial time whether or not the costs of accepting computations is bounded; for
it is decidable in polynomial time whether or not the costs of accepting computations is bounded; for 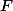 it is decidable in polynomial time whether or not the cardinality of occurring cost sets is bounded. In all three cases we derive explicit upper bounds. For semiring
it is decidable in polynomial time whether or not the cardinality of occurring cost sets is bounded. In all three cases we derive explicit upper bounds. For semiring 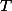 we are able to derive similar results at least in case of polynomials of degree at most 1. For
we are able to derive similar results at least in case of polynomials of degree at most 1. For 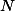 and
and 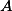 we extend our results to multi-dimensional cost functions.
we extend our results to multi-dimensional cost functions.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
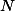 the semiring of nonnegative integers,
the semiring of nonnegative integers, 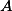 the ldquoarctical semiringrdquo,
the ldquoarctical semiringrdquo, 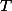 the tropical semiring and
the tropical semiring and 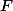 the semiring of finite subsets of nonnegative integers. We show: for semirings
the semiring of finite subsets of nonnegative integers. We show: for semirings 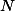 and
and 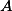 it is decidable in polynomial time whether or not the costs of accepting computations is bounded; for
it is decidable in polynomial time whether or not the costs of accepting computations is bounded; for 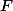 it is decidable in polynomial time whether or not the cardinality of occurring cost sets is bounded. In all three cases we derive explicit upper bounds. For semiring
it is decidable in polynomial time whether or not the cardinality of occurring cost sets is bounded. In all three cases we derive explicit upper bounds. For semiring 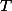 we are able to derive similar results at least in case of polynomials of degree at most 1. For
we are able to derive similar results at least in case of polynomials of degree at most 1. For 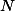 and
and 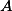 we extend our results to multi-dimensional cost functions.
we extend our results to multi-dimensional cost functions.