Helmut Seidl. Least Solutions of Equations over $\nu$ . In Serge Abiteboul and Eli Shamir, editors, Automata, Languages and Programming, volume 820 of Lecture Notes in Computer Science, pages 400-411, Jerusalem, Israel, July 1994. Springer.

We consider the problem of computing the least solution 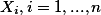$X_{i}, i = 1,..., n$ , of a system of equations 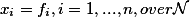$x_{i} = f_{i}, i = 1,..., n, over \mathcal {N}$ , i.e., the naturals (extended by 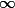$\infty$ ), where the right hand sides 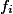$f_{i}$ are expressions built up from constants and variables by operations taken from some set 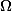$\Omega$ . We present efficient algorithms for various subsets 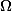$\Omega$ of the operations minimum, maximum, addition and multiplication.

Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com