Kumar Neeraj Verma, Helmut Seidl and Thomas Schwentick. On the Complexity of Equational Horn Clauses. In Robert Nieuwenhuis, editor, Automated Deduction - CADE-20, volume 3632 of Lecture Notes in Computer Science, pages 337-352, Tallinn, Estonia, July 2005. Springer.
Security protocols employing cryptographic primitives with algebraic properties are conveniently modeled using Horn clauses modulo equational theories. We consider clauses corresponding to the class 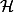 3 of Nielson, Nielson and Seidl. We show that modulo the theory ACU of an associative-commutative symbol with unit, as well as its variants like the theory XOR and the theory AG of Abelian groups, unsatisfiability is NP-complete. Also membership and intersection-non-emptiness problems for the closely related class of one-way as well as two-way tree automata modulo these equational theories are NP-complete. A key technical tool is a linear time construction of an existential Presburger formula corresponding to the Parikh image of a context-free language. Our algorithms require deterministic polynomial time using an oracle for existential Presburger formulas, suggesting efficient implementations are possible.
3 of Nielson, Nielson and Seidl. We show that modulo the theory ACU of an associative-commutative symbol with unit, as well as its variants like the theory XOR and the theory AG of Abelian groups, unsatisfiability is NP-complete. Also membership and intersection-non-emptiness problems for the closely related class of one-way as well as two-way tree automata modulo these equational theories are NP-complete. A key technical tool is a linear time construction of an existential Presburger formula corresponding to the Parikh image of a context-free language. Our algorithms require deterministic polynomial time using an oracle for existential Presburger formulas, suggesting efficient implementations are possible.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
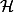 3 of Nielson, Nielson and Seidl. We show that modulo the theory ACU of an associative-commutative symbol with unit, as well as its variants like the theory XOR and the theory AG of Abelian groups, unsatisfiability is NP-complete. Also membership and intersection-non-emptiness problems for the closely related class of one-way as well as two-way tree automata modulo these equational theories are NP-complete. A key technical tool is a linear time construction of an existential Presburger formula corresponding to the Parikh image of a context-free language. Our algorithms require deterministic polynomial time using an oracle for existential Presburger formulas, suggesting efficient implementations are possible.
3 of Nielson, Nielson and Seidl. We show that modulo the theory ACU of an associative-commutative symbol with unit, as well as its variants like the theory XOR and the theory AG of Abelian groups, unsatisfiability is NP-complete. Also membership and intersection-non-emptiness problems for the closely related class of one-way as well as two-way tree automata modulo these equational theories are NP-complete. A key technical tool is a linear time construction of an existential Presburger formula corresponding to the Parikh image of a context-free language. Our algorithms require deterministic polynomial time using an oracle for existential Presburger formulas, suggesting efficient implementations are possible.