Andreas Weber and Helmut Seidl. On the Degree of Ambiguity of Finite Automata. In Jozef Gruska, Branislav Rovan and Juraj Wiedermann, editors, Mathematical Foundations of Computer Science, volume 233 of Lecture Notes in Computer Science, pages 620-629, Bratislava, Czechoslovakia, August 1986. Springer.
We show that the degree of ambiguity of a nondeterministic finite automaton (NFA) with n states, if finite, is not greater than 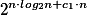 (
(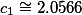 ). We present an algorithm which decides in polynomial time whether the degree of ambiguity of a NFA is finite or not. Additionally, the authors obtain in [14] a corresponding upper bound for the finite valuedness of a normalized finite transducer (NFT), and also a polynomial-time algorithm which decides whether the valuedness of a NFT is finite or not.
). We present an algorithm which decides in polynomial time whether the degree of ambiguity of a NFA is finite or not. Additionally, the authors obtain in [14] a corresponding upper bound for the finite valuedness of a normalized finite transducer (NFT), and also a polynomial-time algorithm which decides whether the valuedness of a NFT is finite or not.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
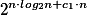 (
(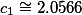 ). We present an algorithm which decides in polynomial time whether the degree of ambiguity of a NFA is finite or not. Additionally, the authors obtain in [14] a corresponding upper bound for the finite valuedness of a normalized finite transducer (NFT), and also a polynomial-time algorithm which decides whether the valuedness of a NFT is finite or not.
). We present an algorithm which decides in polynomial time whether the degree of ambiguity of a NFA is finite or not. Additionally, the authors obtain in [14] a corresponding upper bound for the finite valuedness of a normalized finite transducer (NFT), and also a polynomial-time algorithm which decides whether the valuedness of a NFT is finite or not.