H. Siegel and A. Simon. FESA: Fold- and Expand-based Shape Analysis. Compiler Construction, volume 7791 of LNCS, pages 82--101, Rome, Italy, March 2013. Springer.
A static shape analysis is presented that can prove the absence of NULL- and dangling pointer dereferences in standard algorithms on lists, trees and graphs. It is conceptually simpler than other analyses that use symbolically represented logic to describe the heap. Instead, it represents the heap as a single graph and a Boolean formula. The key idea is to summarize two nodes by calculating their common points-to information, which is done using the recently proposed 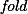 and
and 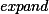 operations. The force of this approach is that both,
operations. The force of this approach is that both, 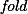 and
and 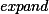 , retain relational information between points-to edges, thereby essentially inferring new shape invariants. We show that highly precise shape invariants can be inferred using off-the-shelf SAT-solvers. Cheaper approximations may augment standard points-to analysis used in compiler optimisations.
, retain relational information between points-to edges, thereby essentially inferring new shape invariants. We show that highly precise shape invariants can be inferred using off-the-shelf SAT-solvers. Cheaper approximations may augment standard points-to analysis used in compiler optimisations.
Download: PDF Reference: Bibtex The original publication is available at www.springerlink.com
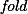 and
and 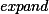 operations. The force of this approach is that both,
operations. The force of this approach is that both, 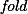 and
and 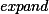 , retain relational information between points-to edges, thereby essentially inferring new shape invariants. We show that highly precise shape invariants can be inferred using off-the-shelf SAT-solvers. Cheaper approximations may augment standard points-to analysis used in compiler optimisations.
, retain relational information between points-to edges, thereby essentially inferring new shape invariants. We show that highly precise shape invariants can be inferred using off-the-shelf SAT-solvers. Cheaper approximations may augment standard points-to analysis used in compiler optimisations.