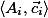 are planar (convex) H-polyhedra, that is,
are planar (convex) H-polyhedra, that is, 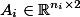 and
and 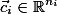 . Let
. Let 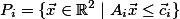 and
and 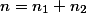 . We present an
. We present an 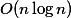 algorithm for calculating an H-polyhedron
algorithm for calculating an H-polyhedron 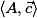 with the smallest
with the smallest 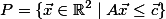 such that
such that 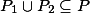 .
.A. Simon and A. King. Convex Hull of Planar H-Polyhedra. International Journal of Computer Mathematics, 81(4):259--271, March 2004.
Suppose 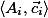 are planar (convex) H-polyhedra, that is,
are planar (convex) H-polyhedra, that is, 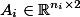 and
and 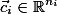 . Let
. Let 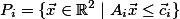 and
and 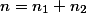 . We present an
. We present an 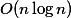 algorithm for calculating an H-polyhedron
algorithm for calculating an H-polyhedron 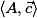 with the smallest
with the smallest 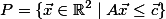 such that
such that 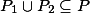 .
.