Helmut Seidl. On the Finite Degree of Ambiguity of Finite Tree Automata. Acta Inf., 26(6):527-542, 1989.
The degree of ambiguity of a finite tree automaton 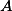 , da(
, da(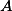 ), is the maximal number of different accepting computations of
), is the maximal number of different accepting computations of 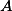 for any possible input tree. We show: it can be decided in polynomial time whether or not da(
for any possible input tree. We show: it can be decided in polynomial time whether or not da(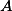 )
)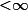 . We give two criteria characterizing an infinite degree of ambiguity and derive the following fundamental properties of an finite tree automaton
. We give two criteria characterizing an infinite degree of ambiguity and derive the following fundamental properties of an finite tree automaton 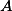 with
with 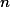 states and rank
states and rank 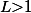 having a finite degree of ambiguity: for every input tree
having a finite degree of ambiguity: for every input tree 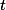 there is a input tree
there is a input tree 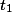 of depth less than
of depth less than 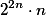 ! having the same number of accepting computations; the degree of ambiguity of
! having the same number of accepting computations; the degree of ambiguity of 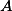 is bounded by
is bounded by 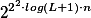 .
.
Download: PDF Reference: Bibtex
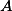 , da(
, da(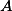 ), is the maximal number of different accepting computations of
), is the maximal number of different accepting computations of 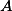 for any possible input tree. We show: it can be decided in polynomial time whether or not da(
for any possible input tree. We show: it can be decided in polynomial time whether or not da(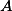 )
)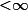 . We give two criteria characterizing an infinite degree of ambiguity and derive the following fundamental properties of an finite tree automaton
. We give two criteria characterizing an infinite degree of ambiguity and derive the following fundamental properties of an finite tree automaton 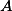 with
with 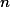 states and rank
states and rank 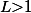 having a finite degree of ambiguity: for every input tree
having a finite degree of ambiguity: for every input tree 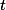 there is a input tree
there is a input tree 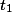 of depth less than
of depth less than 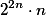 ! having the same number of accepting computations; the degree of ambiguity of
! having the same number of accepting computations; the degree of ambiguity of 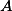 is bounded by
is bounded by 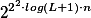 .
.