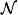Helmut Seidl. Least and Greatest Solutions of Equations over 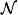$\cal N$ . Nord. J. Comput., 3(1):41-62, 1996.

We consider the problem of computing least and greatest solutions of a system of equations 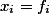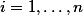$x_i = f_i$ , $i = 1, \ldots, n$ , over 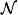$\cal N$ , i.e., the naturals (extended by 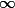$\infty$ ), where the right hand sides 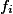$f_i$ are expressions built up from constants and variables by various sets of operations. We present efficient algorithms in case where the following operations occur: (1) minimum and maximum; (2) maximum, addition and multiplication; (3) minimum, addition and multiplication; (4) minimum, maximum, addition and multiplication. We extend the methods to the cases where (one--sided) conditionals are allowed as well.

Download: PDF Reference: Bibtex